Grid Search Optimization for Your Trading Strategy
17 October, 2023
When it comes to algorithmic trading systems, finding the right combination of parameters for your trading strategy is crucial. Grid search optimization is a systematic approach to fine-tune your strategy by testing various hyperparameter combinations. This guide simplifies the process to help you make the most of your trading strategies.
1. Define Your Trading Strategy
Begin by outlining the core elements of your trading strategy. This includes specifying the rules, indicators, and any relevant parameters. A clear strategy is your foundation.
2. Select Hyperparameters to Optimize
Identify which hyperparameters within your strategy need optimization. These could encompass moving average settings, threshold levels, stop-loss and take-profit values, or any other critical factors.
3. Determine Parameter Ranges
For each hyperparameter, set up a range of values to explore. This range should be comprehensive enough to include potential optimal values while avoiding computational complexity.
4. Create a Grid
Construct a grid by combining the values of each hyperparameter. For instance, if you're optimizing two parameters, A and B, each with three potential values, your grid will consist of nine parameter combinations to test.
5. Backtest Each Combination
Implement your trading strategy and backtest it for every combination on historical data. Make sure to factor in transaction costs, slippage, and other trading conditions during this evaluation.
6. Choose a Performance Metric
Select a performance metric to gauge each combination's effectiveness. Common metrics include profit and loss (P&L), Sharpe ratio, maximum drawdown, and win rate, depending on your strategy's objectives.
7. Analyze Results
Review the results from your backtests and pinpoint the combination that outperforms the rest according to your chosen performance metric. Pay attention to factors like risk-adjusted returns and stability.
8. Fine-Tune Parameters
After identifying promising parameter combinations, create a narrower grid centered around those values and repeat the process to further refine your strategy.
9. Out-of-Sample Testing
Validate your strategy's performance in real-world conditions by conducting out-of-sample testing using unseen data. This helps ensure that your strategy remains robust.
10. Regular Reevaluation
Adapt and re-optimize your trading strategies as market conditions change. Remember that past performance does not guarantee future results, and risk management is essential for long-term success.
The Moving Average Crossover Trading Strategy
In this example, we'll optimize the moving average crossover strategy by tuning the short-term and long-term moving average periods.
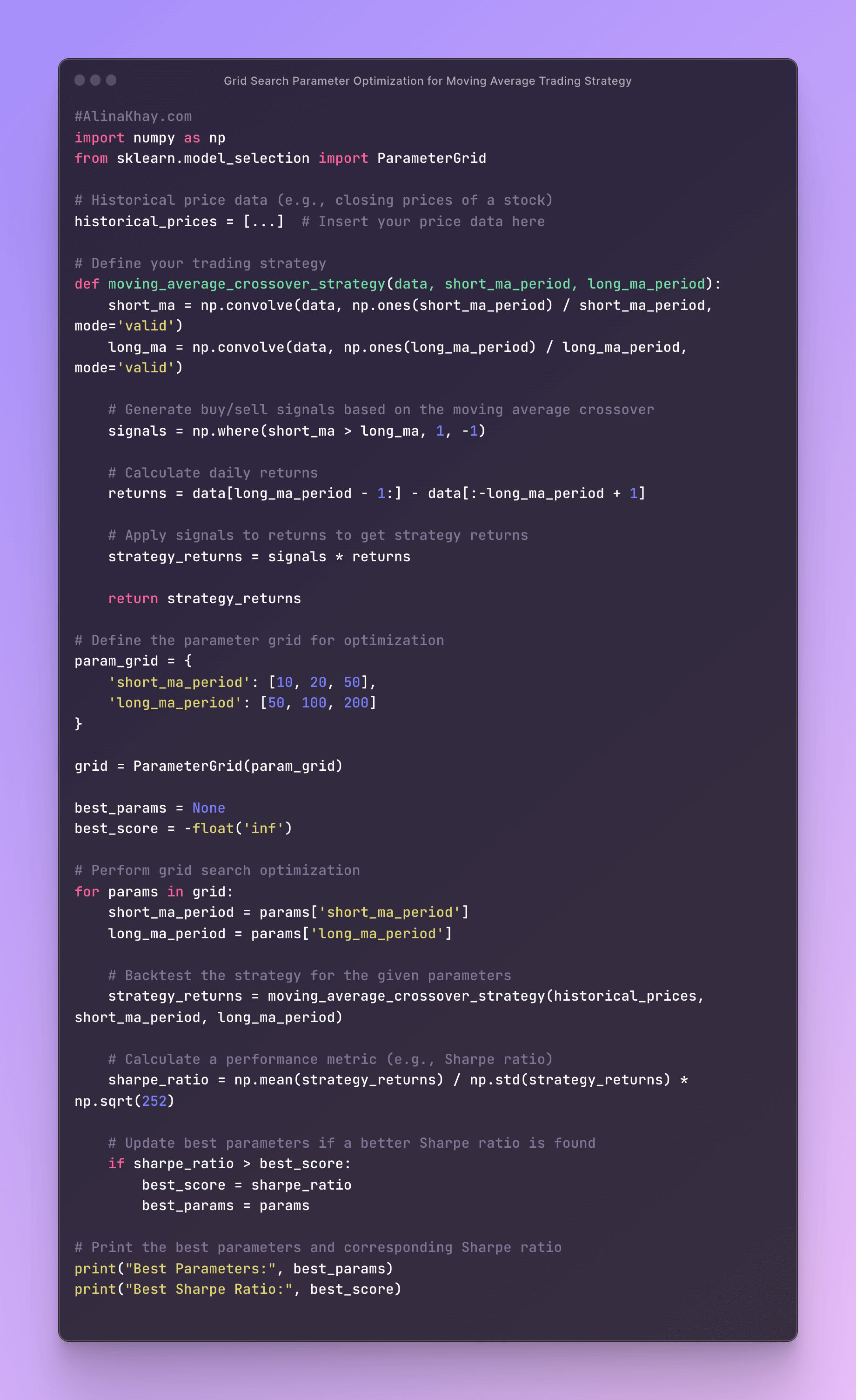
The provided code defines a trading strategy based on a moving average crossover. Here's a description of the strategy and how it works:
Data and Parameters
The strategy assumes you have historical price data for a financial asset (e.g., stock prices) stored in the historical_prices variable. It takes two parameters for the moving averages: short_ma_period and long_ma_period. These parameters represent the time periods for the short-term and long-term moving averages, respectively.
Moving Averages
The moving_average_crossover_strategy function calculates two moving averages: a short-term moving average (short MA) and a long-term moving average (long MA) using the provided historical price data and the specified moving average periods.
Buy/Sell Signals
Buy and sell signals are generated based on the crossover of the short-term and long-term moving averages. When the short-term moving average crosses above the long-term moving average, a buy signal is generated (assigned a value of 1). When the short-term moving average crosses below the long-term moving average, a sell signal is generated (assigned a value of -1).
Daily Returns
Daily returns are calculated based on the historical price data and the moving average periods. Returns are computed as the difference in prices from the start to the end of each trading day.
Strategy Returns
The buy/sell signals generated are applied to the daily returns to calculate the strategy's returns. If a buy signal is present for a particular day, the return for that day is used; otherwise, it's set to zero. This process accounts for the trading decisions based on the moving average crossovers.
Grid Search Optimization
The code sets up a parameter grid for optimization, allowing you to test different combinations of short-term and long-term moving average periods. It performs a grid search by iterating through all parameter combinations in the grid. For each parameter combination, the strategy's returns are backtested, and a performance metric (in this case, the Sharpe ratio) is calculated. The Sharpe ratio is a measure of risk-adjusted returns and helps assess the strategy's performance.
Best Parameters and Sharpe Ratio
The code keeps track of the best parameters that produce the highest Sharpe ratio during the grid search. Once the grid search is complete, the code prints the best parameters and the corresponding Sharpe ratio, indicating the parameter combination that yielded the best risk-adjusted returns.
This strategy is a simple example of how moving averages can be used for trading decisions. The grid search optimization helps identify the optimal combination of short-term and long-term moving average periods that maximize the Sharpe ratio, making it a systematic way to tune the strategy.
Conclusion
In conclusion, while grid search optimization is a valuable approach for refining trading strategies, it's important to use real historical data and explore more advanced objective functions and risk management techniques for a comprehensive assessment.
Additionally, for complex strategies with larger parameter spaces, alternative optimization methods like genetic algorithms or simulated annealing may be more suitable. Remember that grid search has its limitations, including the risk of overfitting to historical data. To address this, employ strategies like cross-validation or walk-forward testing to ensure adaptability to changing market conditions.
Always keep in mind that past performance is not a guarantee of future results, underscoring the need for robust risk management in any trading strategy.